Arrays are the most versatile and commonly used data structures and are built into most programming languages. Arrays are also internally used in defining other data structures such as Stacks, Queues, Hashtables etc.

What are arrays?

Arrays are data storage structures that store data of same type (e.g. char, int, string etc.). Data values stored in the array are commonly referred to as elements of the array.

Structure of Arrays - Arrays are index based, i.e. every element stored in an array has an assigned index number and can be accessed using it's index number. The index of the first element of the array is 0, and the index of the last element of the array is (N-1) where N is the number of elements of the array. N is also referred to as the size of the array.

Arrays are fixed in size, i.e. once you declare an array of a specific length, it's size cannot be changed.

Memory
Memory allocated to an array depends on the size of array and the type of elements. For example, when you create an array of size 10 containing elements of type int (4 bytes), a contiguous memory of 40 bytes (4*10) is allocated for the array.

The array can then be referenced through the address of it's first byte, and an element of the array can be accessed through it's index number.

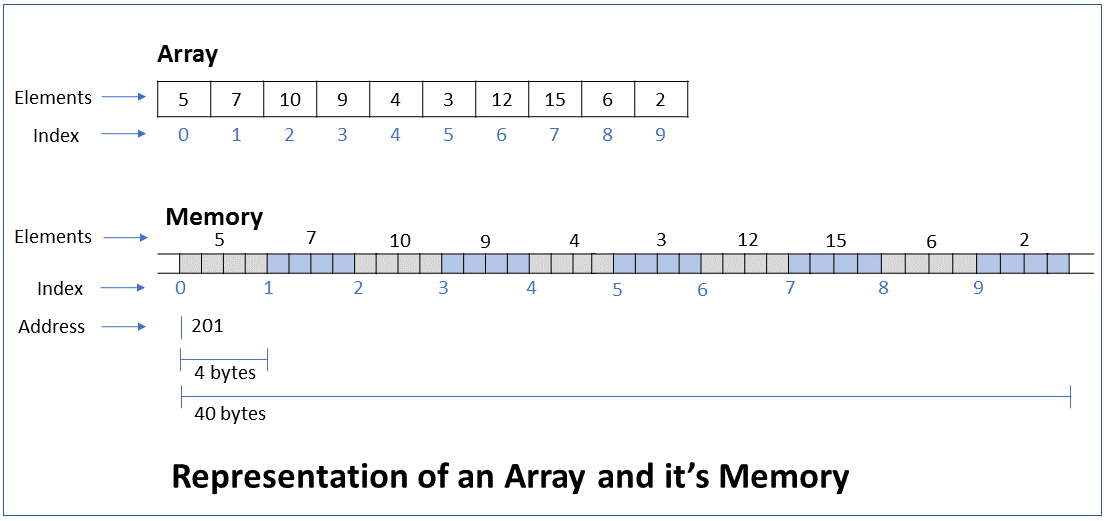
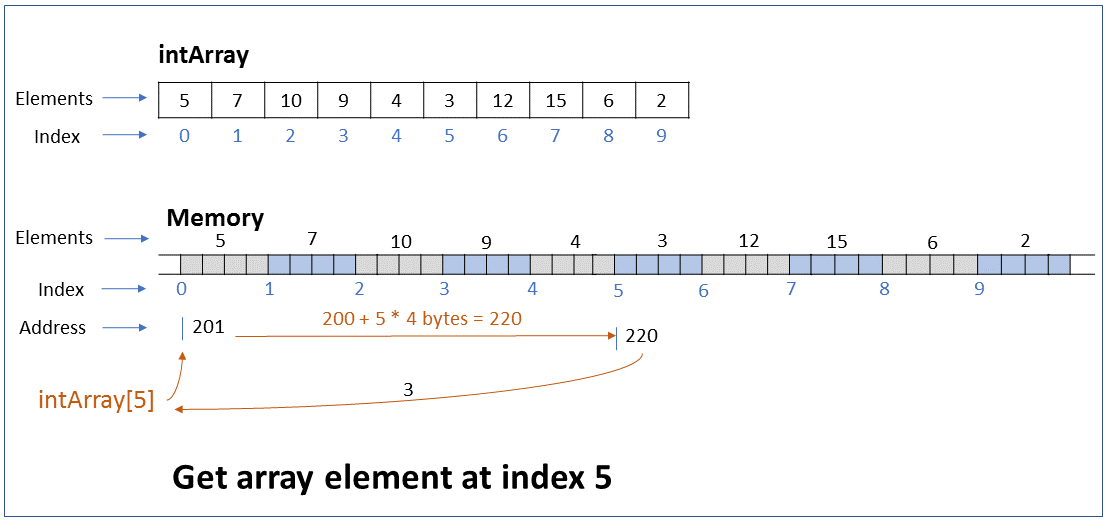
How do you read or update the value of an array element located at a particular index of the array? What is the efficiency of this operation?

The value of an array element can be read or updated by using the index number of the array.

The reference to an array refers to the address of the first byte of the array. When we request access to an element at a particular index, the computer calculates the address of this element based on the element type and index, and returns the element at that address.

For example, if the address of the first node of an int array is 201 and we request access to the element at index 5 (6th element), the computer returns the element at address 220 (200 + 5*4 bytes)

Performance - This operation executes a single step irrespective of the number of elements in the array, i.e. it takes constant time to run. In Big O notation the efficiency is O(1).

//Array of first 10 odd numbers
int[] intArray = {5, 7, 10, 9, 4, 3, 12, 15, 6, 2};

//print the value of array element at index 5
System.out.println(intArray[5]); //prints 3

//update the value of the array element at index 5 
intArray[5] = 21;
System.out.println(intArray[5]);//prints 21

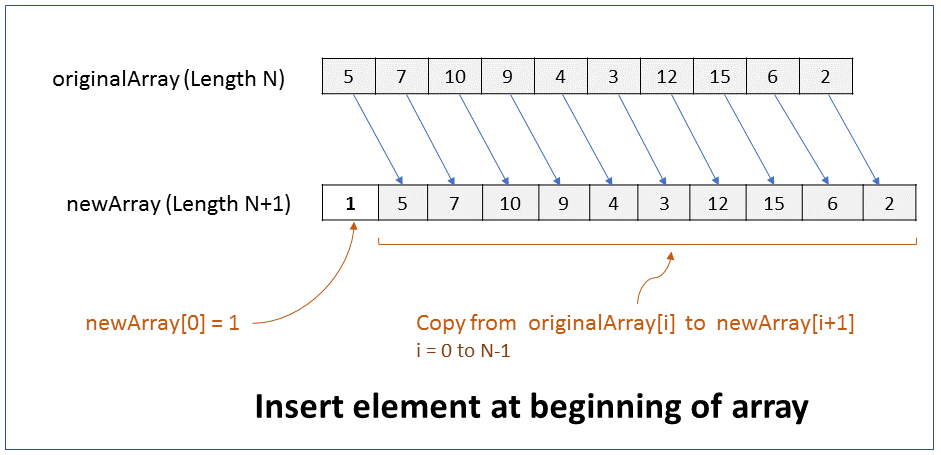
How do you insert an element at the beginning of an array? What is the efficiency of this operation?

The size of an array cannot be changed. Hence, to insert an element at the beginning of an array you have to create a new array of size 1 more than the original array, copy elements from original array to the new array, and then add the new element at index 0 of the new array.

Pseudocode
1. Create new array of size N+1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i+1], where i = 0 to N-1
Add new element at newArray[0]

Performance - For an array of size N, it takes N steps to copy elements from original array to new array. It takes 1 step to add new element at index position 0. Therefore it takes linear time (N+1) to run. In Big O notation the efficiency of this operation is O(N).

//insert an element at the beginning of an array
public static int[] insertBeginning(int[] originalArray, int beginningValue) {
  //create new array with length 1 greater than the original array
  int[] newArray = new int[originalArray.length+1];
  //copy elements from original array to end of new array
  for(int i=originalArray.length-1; i>=0; i--) {
    newArray[i+1] = originalArray[i];
  }
  newArray[0] = beginningValue;
  return newArray;
}

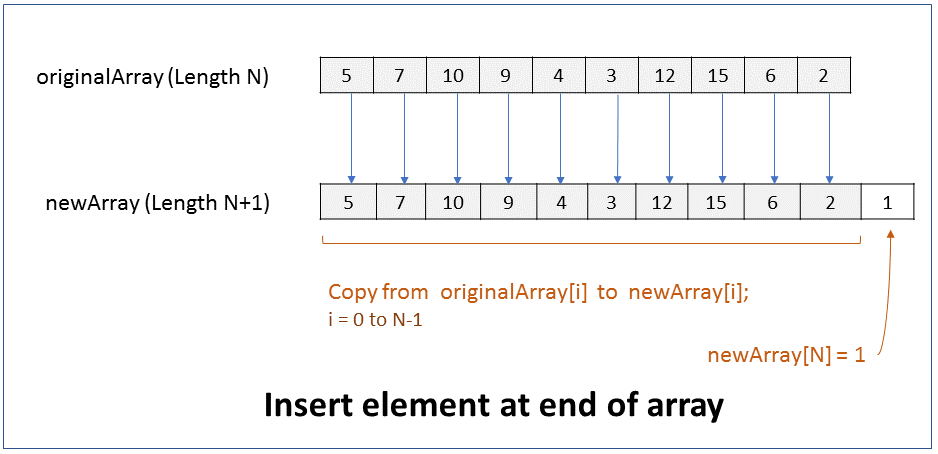
How do you insert an element at the end of an array? What is the efficiency of this operation?

The size of an array cannot be changed. Hence, to insert an element at the end of an array you have to create a new array of size 1 more than the original array, copy elements from original array to the new array, and then add the new element at last index of the new array.

Pseudocode
1. Create new array of size N+1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to N-1
Add new element at newArray[N]

Performance - For an array of size N, it takes N steps to copy elements from original array to new array. It takes 1 step to add new element at last index position 0. Therefore it takes linear time (N+1) to run. In Big O notation the efficiency of this operation is O(N).

//insert an element at the end of an array
public static int[] insertEnd(int[] originalArray, int endValue) {
  //create new array with length 1 greater than original array
  int[] newArray = new int[originalArray.length+1];
  //copy values from original array to beginning of new array
  for(int i=0; i<originalArray.length; i++) {
    newArray[i] = originalArray[i];
  }
  newArray[originalArray.length] = endValue;
  return newArray;
}

How do you insert an element in the middle of an array? What is the efficiency of this operation?

The size of an array cannot be changed. Hence, to insert an element at any index K of an array you have to create a new array of size 1 more than the original array, copy elements from original array to the new array, and then add the new element at index k of the new array.

Pseudocode
1. Create new array of size N+1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to k-1
3. Add new element at newArray[K]
4. Copy from originalArray[j-1] to newArray[j], where j = k+1 to N

Performance - For an array of size N, it takes N steps to copy elements from original array to new array. It takes 1 step to add new element at index position 0. i.e. it takes linear time to run. In Big O notation the efficiency is O(N).

//insert an element at the middle of an array
public static int[] insertMiddle(int[] originalArray, int index, int value) {
  //create a new array of length 1 greater than the original array
  int[] newArray = new int[originalArray.length+1];
  //Copy values from original array to new array 
  //from beginning until the insertion index position
  for(int i=0;i<index;i++) {
    newArray[i] = originalArray[i];
  }
  //insert value
  newArray[index] = value;
  //Copy values from original array to new array
  //from index+1 until the last position
  for(int i=index+1; i<=originalArray.length; i++) {
    newArray[i] =originalArray[i-1];
  }
  return newArray;
}

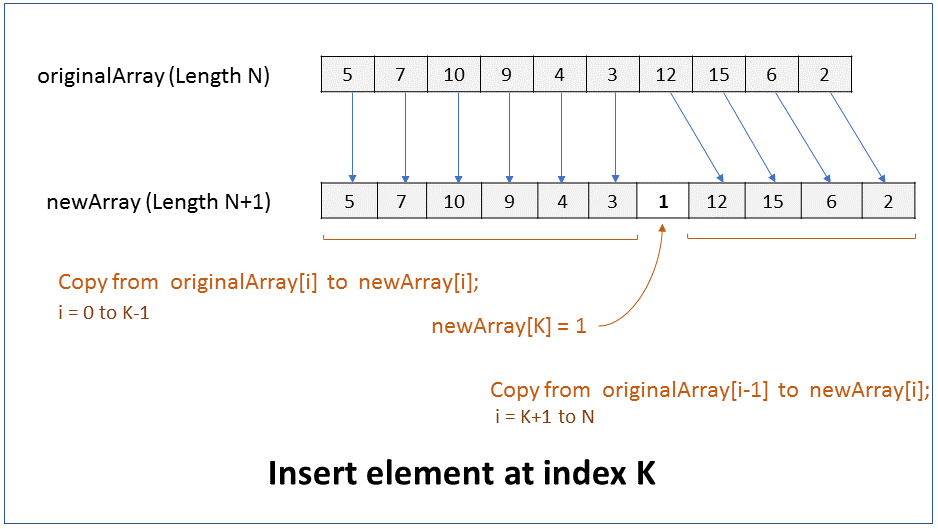
How do you delete an element from the beginning of an array? What is the efficiency of this operation?

We will assume that the size of the array must reduce by 1 after the element is deleted. i.e. there should not be a gap or hole in the array after the element is deleted.

The size of an array cannot be changed. Hence, to delete an element from the beginning of an array you have to create a new array of size 1 less than the original array, and copy all elements from original array to the new array except for the first element.

Pseudocode
1. Create new array of size N-1, where N is size of original array.
2. Copy from originalArray[i+1] to newArray[i], where i = 0 to N-1

Performance - For an array of size N, it takes N-1 steps to copy elements from original array to new array, ignoring the first element. Therefore it takes linear time (N-1) to run. In Big O notation the efficiency of this operation is O(N).

//delete an element from the beginning of an array
public static int[] deleteBeginning(int[] originalArray) {
  //Create new array of length 1 less that the original array
  int[] newArray = new int[originalArray.length-1];
  for(int i=0; i<originalArray.length-1; i++) {
    newArray[i] = originalArray[i+1];
  }
  return newArray;
}

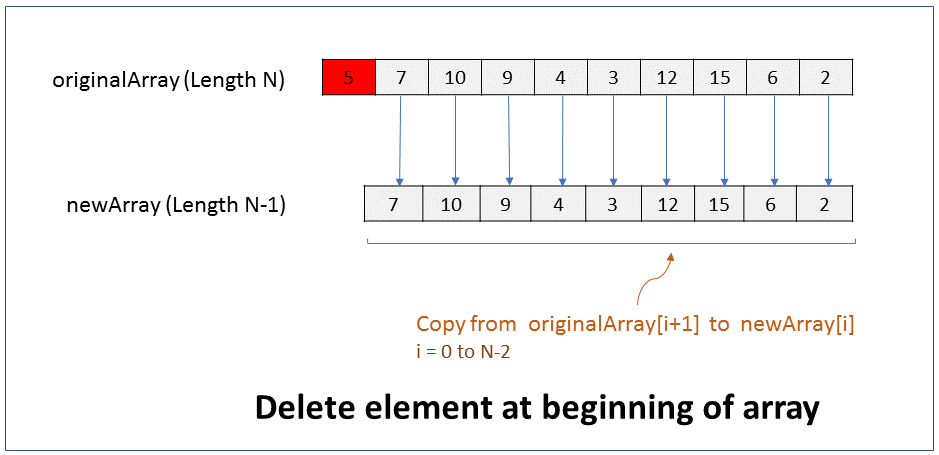
How do you delete an element from the end of an array? What is the efficiency of this operation?

We will assume that the size of the array must reduce by 1 after the element is deleted. i.e. there should not be a gap or hole in the array after the element is deleted.

Since the size of an array cannot be changed, to delete an element from the beginning of an array you have to create a new array of size 1 less than the original array, and copy all elements from original array to the new array except for the last element.

Pseudocode
1. Create new array of size N-1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to N-2

Performance - For an array of size N, it takes N-1 steps to copy elements from original array to new array, ignoring the last element. Therefore it takes linear time (N-1) to run. In Big O notation the efficiency of this operation is O(N).

//delete an element from the end of an array
public static int[] deleteEnd(int[] originalArray) {
  //create new array of length 1 less than the original array
  int[] newArray = new int[originalArray.length-1]; //
  //copy values from old array to new array //
  for (int i=0; i<originalArray.length-1; i++ ) {
    newArray[i] = originalArray[i];
  }
  return originalArray;
}

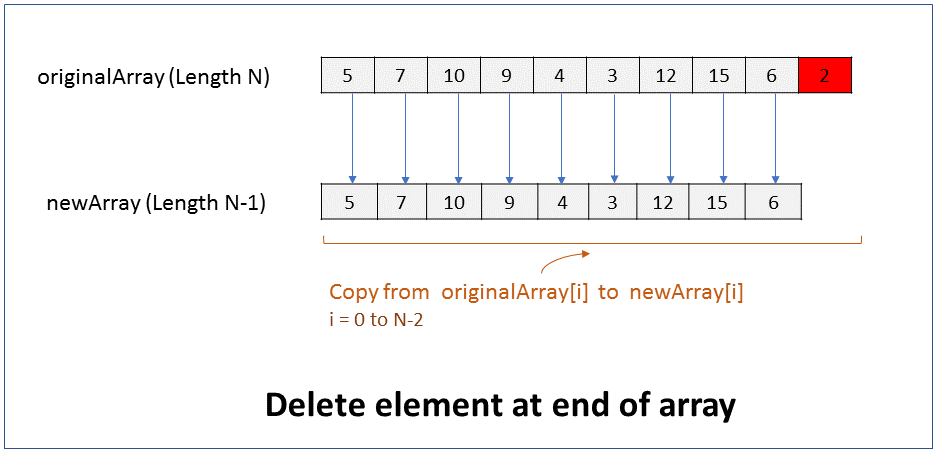
How do you delete an element in the middle of an array? What is the efficiency of this operation?

We will assume that the size of the array must reduce by 1 after the element is deleted. i.e. there should not be a gap or hole in the array after the element is deleted.

Since the size of an array cannot be changed, to delete an element from the beginning of an array you have to create a new array of size 1 less than the original array, and copy all elements from original array to the new array except for the element that has to be deleted.

Pseudocode
1. Create new array of size N-1, where N is size of original array.
2. Copy from originalArray[i] to newArray[i], where i = 0 to k-1
3. Copy from originalArray[j-1] to newArray[j], where j = k+1 to N

Performance - For an array of size N, it takes N-1 steps to copy all elements from original array to new array except for the element to be deleted. In Big O notation the efficiency is O(N).

//delete an element from the middle of an array
public static int[] deleteElement(int[] originalArray, int index) {
  //create new array of length 1 less than the original array
  int[] newArray = new int[originalArray.length-1];
  //loop through the array and copy elements from old array to new array until index
  for (int i=0; i<index; i++) {
    newArray[i] = originalArray[i];
  }
  //shift elements to left after index K
  for (int j=index;j<originalArray.length-1; j++)  {
    newArray[j] = originalArray[j+1];
  }
  return newArray;
}

How do you search an element from an array? What is the efficiency of this operation?

There are two kinds of searches that can be performed on arrays - Linear search and Binary search. Binary search is more efficient than linear search, but it can be performed only on sorted arrays.

Linear search - For unsorted arrays you can use linear search to find an element.

In linear search you loop through the array and compare the value of each element against the search value.

Performance - For an array of size N, it takes an average of N/2 steps to complete the operation. In the best case scenario if the match is found in the first element then only 1 step is used. In the worst case scenario if the elements exists at the end of the array, or if the element does not exist, then it takes N steps to perform the search operation.

The time efficiency of this operation in Big-O notation is O(N).

Binary search - For sorted arrays you can use binary search to search for an element.

In binary search you compare the search value with the value of the middle element of the array.
- If the search value is smaller then you compare the search value with the middle element of the first half of the array.
- If the search value is larger then you compare the search value with the middle element of the second half of the array.
- You continue this process until the element is found.

Performance - It takes log(N) steps to complete this operation. The time efficiency of this operation in Big-O notation is O(log N).

Write a function to search an array using linear search.

In a linear search you loop through the array element by element until the search value is found. In this function we assume that either duplicates are not allowed or you stop the search once the search value is found. Below is the code snippet for linear search.

The time complexity of this search is O(N).

public int findIndex(int searchKey, int[] intArray) {
 int foundIndex=-1;
 for(int i=0; i<intArray.length; i++) {
  if(intArray[i]==searchKey) {
    foundIndex = i;
    break;
  } 
 }
 return foundIndex;
}

Write a function to search an array using binary search.

In a binary search you compare the search value with the value of the middle element of the array.
- If the search value is smaller then you compare the search value with the middle element of the first half of the array. If the search value is larger then you compare the search value with the middle element of the second half of the array. You continue this process until the element is found. Below is the code snippet for binary search

The time complexity of this search is O(log N).

public int findIndex(int searchKey, int[] intArray) {
 int lowerBound = 0;
 int upperBound = intArray.length - 1;
 int currentIndex;
 while(true) {
  currentIndex = (lowerBound + upperBound)/2
  if(intArray[currentIndex]==searchKey) {
    return currentIndex;
  } else if(lowerBound > upperBound){
    //value not found
    return -1;
  } else if(intArray[currentIndex] < searchKey){
    //value in upper half
    lowerBound = currentIndex + 1;
  } else if(intArray[currentIndex] > searchKey){
    //value in lower half
    upperBound = currentIndex - 1;
  }
 }
}

How do you sort the elements in an array?

Sorting of data is an important concept in computer science. It is a preliminary step for many algorithms. For example - binary search which is much faster than linear search, requires data to be sorted before the binary search algorithm can be applied to data.

Extensive research and work has gone into this subject in computer science, resulting in improved and efficient sort algorithms along the years.

Following are the common sort algorithms that you have to know for your interview. Following questions address each of these sort algorithms.

1. Bubble Sort
2. Selection Sort
3. Insertion Sort
4. Shellsort
5. Quicksort
6. Radixsort

How do you sort the elements in an array using Bubble Sort algorithm?

Bubble sort is the simplest of sort algorithms but is also the slowest. It is a good algorithm to begin learning sorting techniques.

Approach
1. Start from the left of the array, i.e. index position 0.
2. Compare with the value at the next position, i.e. index 1. If the value at index 0 is greater than the value at index 1, then swap them.
3. Repeat step 2 for all adjacent pairs of values until the end of array is reached. At this point the last index of the array contains the highest value.
4. Repeat steps 1, 2, 3 until the whole array is sorted.

Performance - The time efficiency of Bubble sort operation in Big-O notation is O(N*2).

How do you sort the elements in an array using Selection Sort algorithm?

Selection Sort improves on the Bubble Sort by reducing the number of swaps from O(N*2) to O(N). The number of comparisons remain O(N).

Approach
1. Start from the left of the array, i.e. index position 0, and pass through all elements and select the smallest number. Swap the smallest number with number at position 0.

2. Start from the next position of the array, i.e. index position 1, and pass through all subsequent elements and select the smallest number. Swap the smallest number with number at position 1.

Repeat for all remaining elements, i.e. elements at index positions 2,3,4... until the last element of the array.

Performance - The time efficiency of Selection sort operation in Big-O notation is O(N*2).

How do you sort the elements in an array of numbers using Insertion Sort algorithm?

Insertion Sort works by marking an element as a marker element and partially sorting all numbers to the left of this marker element. We then insert the marker element and each element to the right of the marker element at the appropriate position in the partially sorted array.

Approach
1. Start by selecting one of the elements, usually an element in the middle of the array, as a marker element.

2. Sort all the elements to the left of the marker element.

3. Insert the marker element at appropriate position in the sorted array such that the sort order is maintained. Shift all elements with a value greater than the marker element one position to the right to make way for the marker element.

4. Repeat step 3 for each of the elements to the right of the marker element.

Performance - - The time efficiency of Insertion sort operation in Big-O notation is O(N*2).

How do you sort the elements in an array of numbers using Quick Sort algorithm?

Quicksort is the fastest in-memory sort algorithm in most situations. Quicksort algorithm works by partitioning an array into two subarrays, and the recursively calling itself to sort the subarrays.

Approach
1. Partition the array into left and right subarrays.
2. Call recursively to sort the left subarray
3. Call recursively to sort the right subarray.

Performance - - The time efficiency of Insertion sort operation in Big-O notation is O(N*logN).

Find largest number in an array of integers.

Given an array of integers, find the largest number in the array.

See Solution >>

Find smallest and largest number in an array of integers.

Given an array of integers, find the smallest and the largest number in the array.

See Solution >>

Find the running sum of an array of integers.

Given an array of integers, return a new array containing the running sum of integers of first array.

See Solution >>

Find count of numbers that are smaller than the current number.

Given an array of integers, return a new array containing the count of numbers that are less than the current number.

See Solution >>

Find the sum of digits of the smallest number in an array.

Given an array of integers, find the sum of digits of the smallest number in the array.

See Solution >>

Find the pivot index in an array of integers.

Given an array of integers, find the index (pivot index) where the left sum equals the right sum.

See Solution >>

Interview questions on Linked lists are the second most frequently asked data structure questions, next only to Arrays.

What are Linked Lists?

Linked lists are data structures in which each data element has a link or reference to the next data element.

Each data item in a linked list is embedded in a link, which is an object of a class called Link. Link contains the data item and in addition contains a reference to the next link object in the data structure.

Unlike arrays, the data elements in linked lists cannot be accessed directly using an index. The only way to access an element in a linked list is to traverse link by link until you get to the element.

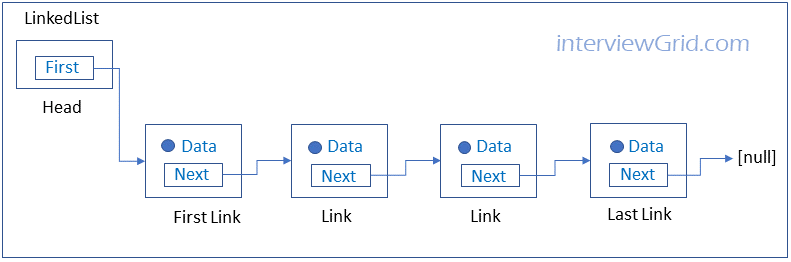
Write a Link class.

A link class contains the data item and a reference to the next data element. Below code snippet is a link class written in Java programming language containing a data element of type int.

class Link {
 //data item
 public int intData;
 //reference to next link
 public Link next;

 public Link(int data) {
  this.intData = data;
 }
}

Write a LinkedList class with method to insert an item in the first position of the LinkedList.

A LinkedList class contains a reference to the first link on the list. Rest of the data items of the linked list are retrieved by using the first item.

Pseudocode
1. Create a new Link link1 that has to be inserted at the first position of the LinkedList.
2. Set link1.next to first.
Set first to link1.

class LinkedList {
  private Link first;
  //constructor
  public void LinkedList() {
  this.first = null;
 }
 //insert an element at start of list
  public void insertFirst(int data) {
    Link link = new Link(data);
    link.next = first;
    first = link;
 }
}

Write a LinkedList class with method to delete the first link in the LinkedList.

A LinkedList class contains a reference to the first link on the list. Rest of the data items of the linked list are retrieved by using the first item.

Pseudocode
1. Set temp to first.
2. Set first to temp.next.

class LinkList {
  private Link first;
  //constructor
  public void LinkList() {
    this.first = null;
  }
  //delete an element from start of list
  public void deleteFirst(){
    Link temp = first;
    first = temp.next;
  }
}

Write a LinkList class with method to search items in the list.

Below Java code snippet includes the find() method added to the LinkList class which searches an item in the linked list.

class LinkList {
 private Link first;
 //constructor
 public void LinkList() {
  this.first = null;
 }
 //search for an item
 public Link find(int key){
  Link current = first;
  while (current.intData!=key) {
    if (current.next==null) {
      return null;
    } else {
      current = current.next;
    }
  }
   return current;
 }
}

Write a LinkList class with method to delete items in the list.

Below Java code snippet includes the delete() method added to the LinkList class which deletes an item in the linked list.

class LinkList {
 private Link first;
 //constructor
 public void LinkList() {
  this.first = null;
 }
 //insert an element at start of list
 public voidinsertFirst(int data) {
  Link link = new Link(data);
  link.next = first;
  first = link;
 }
 //delete an element from start of list
 public void deleteFirst() {
  Link temp = first;
  first = temp.first;
 }
 public Link find(int key) {
  Link current = first;
  while (current.intData!=key) {
    if (current.next==null) {
      return null;
    } else {
      current = current.next;
    }
  }
   return current;
 }
 public Link delete(int key) {
  Link current = first;
  Link previous = first;
  while (current.intData!=key) {
    if current.next==null) {
      return null;
    } else {
      previous = current;
      current = current.next;
    }
  }
  if(current == first) {
    first =first.next;
  } else {
    previous.next = current.next;
  }
   return current;
 }
}

What is the time efficiency of insertion, deletion and searching in linked lists.

Insertion or deletion of an element from the front of the linked list is fast and takes O(1) time. I.e it takes a constant time and is not dependent on the number of data elements in the linked list.

Insertion or deletion of a data element, which is not the first element, takes linear time O(N). I.e the time efficiency linearly depends on the number of elements in the linked list.

Searching for an element in the linked list takes linear time ON(N). I.e the the time efficiency linearly depends on the number of elements in the linked list.

What are the advantages of linked lists over arrays?

In linked lists elements do not have to be moved after an element is inserted or deleted.. In arrays elements have to be moved after an element is inserted or deleted. Hence insert and delete operations are more efficient in linked lists compared to arrays.

The size of an array is fixed when it is initially created. This leads to inefficiencies since the array usually turns out to be too big or small. Linked lists uses exactly as much memory as needed, and can dynamically expand to use more memory as more elements are added to the linked list.

Stacks are abstract data structures that allow access to only one data item - the last item inserted. Stacks are abstract since they internally use other data structures, such as arrays, and provide interfaces to restrict access to the items

What are stacks?

Stacks are programmatic data structures that allow access to only one item at a time, the last item inserted. Stacks internally use other data structures such as arrays for their implementation. A stack is a Last-In-First-Out (LIFO) storage mechanism, because the last item inserted is the first to be removed.

What are the key public interfaces provided by Stacks?

Stacks usually provide the following key interfaces.

push() - Inserts a new data item on the top of the stack.

pop() - Removes the item from the top of the stack

peek() - Returns the item from the top of the stack without removing it.

isFull() - Returns true if the stack is full.

isEmpty() - Returns true if the stack is empty.

Write a program to implement stack functionality?

Following Java program implements the stack functionality. It internally uses an array for the implementation.

class MyStack {

 private int maxSize;
 private int[] stackArray;
 private int top; //constructor
 public MyStack(int maxSize) {
  this.maxSize = maxSize;
  stackArray = new int[maxSize];
  top = -1;
 }

 //push an item to stack
 public void push(int i) {
  //increment top and insert item
  stackArray[++top] = i;
 }

 //remove an item from stack
 public void pop() {
  //return item and decrement top
  return stackArray[top--] = i;
 }

 //view item from top of stack
 public void peek() {
  return stackArray[top];
 }

 //check if stack is empty
 public void isEmpty() {
  return (top == -1);
 }

 //check if stack is full
 public void isFull() {
  return (top == maxSize);
 }
}

What is the time efficiency of the push() and pop() operations of stacks?

The push() and pop() methods implemented in stacks take constant time to execute. i.e. the time to execute is very quick and is not dependent on the number of items on the stack. In Big O notation this is represented as O(1).

What are some common scenarios where stacks are used?

Following are some of the common scenarios in which Stacks can be Used.

- To check if delimiters (parenthesis, brackets etc.) are balanced in a computer program

- To reverse strings

- To traverse the nodes of a binary tree.

- To search the vertices of a graph.

- To process tasks

- To process messages

What are queues?

Queues are programmatic data structures that allow access to only one item at a time, the first item inserted. Queues internally use other data structures such as arrays for their implementation. A queue is a First-In-First-Out (FIFO) storage mechanism, because the first item inserted is the first to be removed.

What are the key public interfaces provided by queues?

Queues usually provide the following key interfaces.

insert() - Inserts a new data item oat the end of queue.

remove() - Removes the item from the end of the queue

peek() - Returns the item from the front of the queue without removing it.

isFull() - Returns true if the queue is full.

isEmpty() - Returns true if the queue is empty.

Write a program to implement queue functionality?

Following Java program implements the queue functionality. It internally uses an array for the implementation.

class MyQueue {

 private int maxSize;
 private int[] queueArray;
 private int front;
 private int rear;
 private int numberOfItems;

 //constructor
 public MyQueue(int maxSize) {
  this.maxSize = maxSize;
  queueArray = new int[maxSize];
  front = 0;
  rear = -1;
numberOfItems = 0; }

 //insert an item to queue
 public void insert(int i) {
  //increment rear and insert item
  queueArray[++rear] = i;
  nItems++;
 }

 //remove an item from queue
 public int remove() {
  //return item and decrement top
  int temp = queueArray[front++];  nItems--;
  return temp;
 }

 //view item from top of stack
 public void peek() {
  return queueArray[front];
 }

 //check if stack is empty
 public void isEmpty() {
  return (numberOfItems== -1);
 }

 //check if stack is full
 public void isFull() {
  return numberOfItems == maxSize);
 }
}

What is the time efficiency of the push and pop implementations of queues?

The push() and pop() methods implemented in stacks take constant time to execute. i.e. the time to execute is very quick and is not dependent on the number of items on the stack. In Big O notation this is represented as O(1).

What are some common scenarios where queues are used?

Following are some of the common scenarios in which Stacks can be Used.

- To check if delimiters (parenthesis, brackets etc.) are balanced in a computer program

- To reverse strings

- To traverse the nodes of a binary tree.

- To search the vertices of a graph.

What are Deques?

Deques are double-ended queues in which you can insert items either at the front or rear, and can delete items either from the front or rear. Deques provide the methods similar to insertLeft(), insertRight(), removeLeft() and removeRight() to insert and remove from both ends.

What are Priority Queues?

A priority queue is a specialized queue in which the items are ordered, so that the lowest (or highest) key is always in the front. So when you get an item from a priority queue then you always get the lowest value item (or highest value item based on how the items are ordered).

Write a program to implement priority queue functionality?

Following Java program implements the priority queue functionality. It internally uses an array for the implementation. The array items are ordered in ascending order, and the insert() function inserts an item in the correct position in the array.

class MyPriorityQueue {

 private int maxSize;
 private int[] queueArray;
 private int numberOfItems;

 //constructor
 public MyPriorityQueue(int maxSize) {
  this.maxSize = maxSize;
  queueArray = new int[maxSize];
numberOfItems = 0; }

 //insert an item to queue
 public void insert(int i) {
  //increment rear and insert item
  if(numberOfItems==0){
    queueArray[numberOfItems] = i;
  } else {
    for(int j=numberOfItems-1; j>=0; j--) {
      if(i > queueArray[j]) {        queueArray[j+1] = queueArray[j];      } else {        break;      }    }    queueArray[++rear] = i;
    nItems++;
  }
 }

 //remove an item from queue
 public int remove() {
  //return item and decrement count
  return queueArray[--numberOfItems]; }

 //view item from top of stack
 public void peek() {
  return queueArray[numberOfItems-1];
 }

 //check if stack is empty
 public void isEmpty() {
  return (numberOfItems == 0);
 }

 //check if stack is full
 public void isFull() {
  return (numberOfItems == maxSize);
 }
}

Questions on binary trees are very frequently asked in interview questions.

What are Trees?

Trees are data structures that consist of nodes that are connected by edges.

Nodes can represent real world entities such as people, houses, cities etc. Edges represent the relationship between the nodes.

Typically there is a single node at the top row of the tree, more on the second row, and gradually increasing as we go down the rows of the tree.

Tree Terminology

Root - Root is the top node of a tree. A tree can have only one root. Every node must have only one path to the root of the tree.

Edge - Edge is the line connecting from one node to another

Path - Path is the connection from one node to another along the edges, and spanning multiple nodes.

Parent - Every node has an edge going upwards and connecting to another node called as its parent node.

Child - Every node can have one or more edges going downwards and connecting to nodes called child nodes.

Leaf - a node that does not have child nodes is called a leaf node.

Key - The data value represented by a node is called the key.

Tree Representation

Nodes in a tree are represented by circles containing the key value. Edges are represented as lines between the circles.

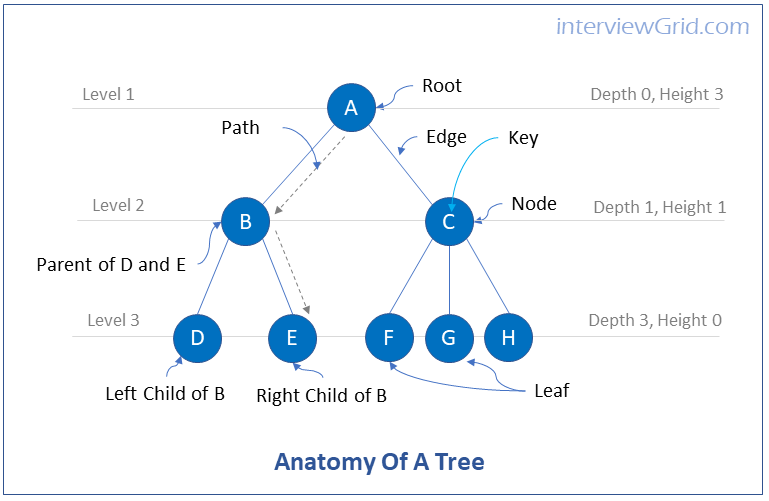
What are binary trees?

Binary trees are trees in which each node has at most two child nodes. The child node on the left is called the left child node and the child node on the right is called the right child node.

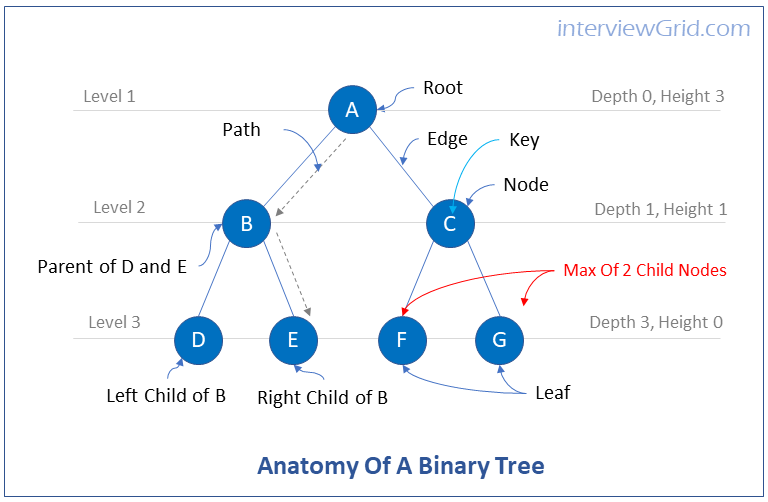
What are binary search trees?

Binary search trees are binary trees in which a parent node's left child must have a key less than the parent node, and a parent node's right child must have a key greater than the parent node.

Advantages of Binary Search Trees

Binary search trees have the advantages of both ordered arrays and linked lists.

Searches are quick with ordered arrays, but insertions and deletions are slow. Insertions and deletions are quick with linked lists, but searches are slow.

Searches, insertions and deletions are fast with binary search trees.

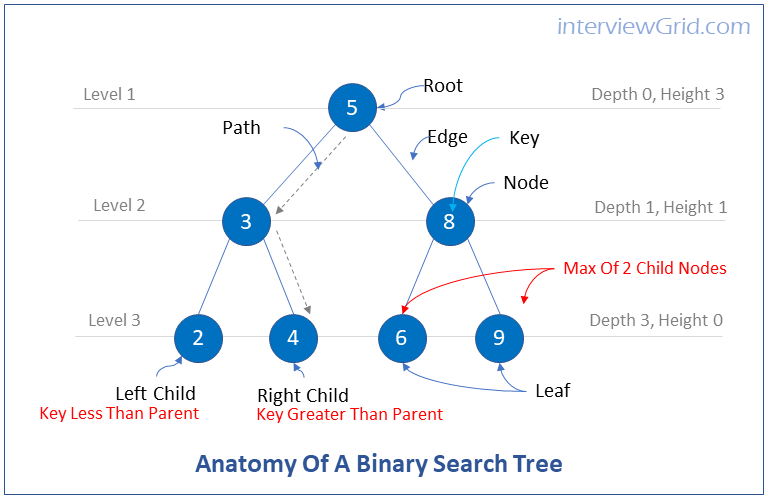
What is the difference between balanced vs Unbalanced binary tree?

In balanced trees there are approximately equal number of left descendant nodes and right descendant nodes. In unbalanced trees there are many more left descendant nodes than right descendant nodes, or vice versa.

What are the key operations performed on binary tree? What is their time efficiency

Insertions, Deletions, Searches are the common operations performed on binary search trees.

The time efficiency of these operation on binary search trees is O(logN)

Write code to represent the node in a binary search tree.

The node in a binary search tree has 4 key elements.
1. Key
2. Data
3. Reference to left child node
4. Reference to right child node

//Node
public class Node {
  public int key;
  public int data;
  public Node leftChild;
  public Node rightChild;
  //constructor
  public Node(int key, int data) {
    this.key = key;
    this.data = data;
    this.firstChild = null;
    this.rightChild = null;
  }
}

What are the key operations performed on binary tree? What is their time efficiency

Insertions, Deletions, Searches are the common operations performed on binary search trees.

The time efficiency of these operation on binary search trees is O(logN)

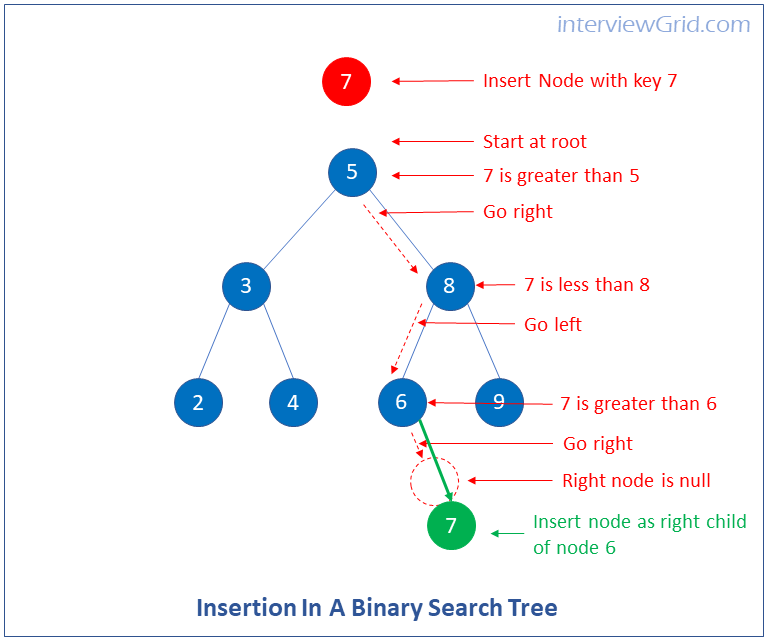
How do you insert a node in a binary search trees? Write a function to insert a node in a binary search tree.

You can insert a new node in a binary tree by traversing the binary tree and finding the position to insert the node, i.e. finding the parent node for the new node to be inserted. You can then insert the new node by making it a child node of the parent node.

Pseudocode
1. Start with the root (current node). If root is null then root = new node.
2. If key of new node is less than key of root then go to left node, else go to right node. this becomes the current node
3. If key of new node is less than current node then go to left child, else go to right child.
4. Repeat step 3 until current node is null.
5. If current node is left of parent node insert the new node here by referring the left child of parent node to new node.
6. If current node is right of parent node, insert the node here by referring the right child of the parent node to the new node.

How do you perform searches on binary search trees? Write a function to find a node in a binary search trees.

Following are key steps to perform searches on binary search trees.

1. Start at the root node and compare its value to the search key value.
2. If the search key value is less than the node value then go to the node's left child.
3. If the search key value is greater than the node value then go to the node's right child.

4. Repeat above steps for every child node that is visited.

How do you perform deletions on binary search trees? Write a function to delete from binary search trees.

Following are the key steps to perform insertions on binary search trees.

Perform search operation on the binary tree until the node to be deleted is found. The next steps depends on the number of child nodes that this node has. There are three possibilities

1. Node to be deleted has no children - If the node to be deleted has no children, i.e it is a leaf node, then just set the corresponding child reference (left child or right child) in the parent node to null.

2. Node to be deleted has one child - If the node to be deleted has only one child (say Node A), then set the corresponding child reference (left child or right child) in the parent node to this child node (Node A)

3. Node to be deleted has two children - If the node to be deleted has two children then replace the node with its in-order successor. The in-order successor is either the right child of the node to be deleted, or it can be a left descendant to right child of the node to be deleted.
A: In-order successor is the right child of the node to be deleted.
- Set the right child field (or left child field) of the parent node to the successor node.
- Set the left child field of the parent node to the left child field of the node to be deleted.
B: In-order successor is a left descendant to the right child of the node to be deleted
- successorParent.leftChild = successor.rightChild
- successor.rightChild = delNode.rightChild
parent.rightChild = successor
- successor.leftChild = current.leftChild

Questions on red-black trees are very frequently asked in interview questions.

What are red-black trees? What problem do they solve

Binary search trees work well when they are ordered and balanced. But when new items are inserted into an ordered binary search tree, the binary search tree becomes unbalanced. With unbalanced trees the efficiency of searches degrades.

Red-black trees are specialized binary search trees with additional features which ensures that the trees are balanced.

How are red-black trees maintained in a balanced state?

Red-black trees are balanced during insertion and deletion od items to the tree. The insertion and deletion routines of the red-black tree check that certain characteristics of the tree are not violated. If these characteristics are violated, the routines re-structure the tree so that the tree remains in a balanced state.

What are the characteristics of red-black trees?

Following are the two characteristics of red-black trees.

1. Colored nodes: The nodes in a red-black tree are colored. Each node can be either red or black.

2. Red-black rules: When a node is inserted or deleted in a red-black tree. certain rules have to be followed to ensure that the tree remains balanced after the node deletion or insertion.

What are the rules that have to be followed when an item is inserted or deleted from a tree?

Followed are the rules that must be followed when a node is inserted or deleted from a red-black tree.

1. Every node is either a red node or a black node

2. The root node of the red-black tree is always black.

3. If a node is red then is child nodes must be black. The converse is not true. I.e. if a node is black then its child nodes can either be red or black.

4. Every path from the root node to a leaf node, or to a null node, must contain the same number of black nodes.

How do you fix rule violations when a node is inserted or deleted from a red-black tree?

There are two ways to fix rule violations in red-black trees.

1. Fix rule violations by changing the color of nodes.

2. Fix rule violations by performing rotations. A rotation is rearrangement of nodes that makes the tree more balanced.

What is the time efficiency of insertion, deletion and search operations on red-black trees?

Insertions, deletions and searches are the common operations performed on red-black trees.

The time efficiency of these operation on binary search trees is O(logN).

2-3-4 trees is an advanced topic on data structures and interview questions on this topic may be asked for senior positions.

What are multiway trees?

Multiway trees are trees in which the nodes have more data items and children than a binary tree. I.e each node in a multiway tree can have more than one data item, and more than two children.

What are 2-3-4 trees?

2-3-4 trees are multiway trees in which each node has up to three data items and four children. Since nodes in a 2-3-4 tree can have up to four children they are multiway trees of order four.

2-3-4 trees are balanced trees similar to red-black trees.

What is the relationship between the number of data items and the number of children that a node can contain in a 2-3-4 tree?

Following is the relationship between the number of data items and the number of children that a node can contain in a 2-3-4 tree.

1. A node with one data item must have two children.

2. A node with two data items must have three children

3. A node with three data items must have four children.

A leaf node does not have children but can have up to three data items.

Can a node in a 2-3-4 tree have a single child node?

No, a node in a 2-3-4 tree cannot have a single child. Each node must have a minimum of two nodes and if it is leaf node then it does not have any child nodes.

What is the relationship between the key values of data items in a node to its child nodes?

No, a node in a 2-3-4 tree cannot have a single child. Each node must have a minimum of two nodes and if it is leaf node then it does not have any child nodes.

How are nodes organized is a 2-3-4 tree?

The data items in a node are arranged in ascending key order from left to right. The data items in a node are numbered as 0, 1 and 2 for convenience.

Following is the principle by which nodes are organized in a 2-3-4 tree.

All children in the subtree rooted at child 0 have key values less than key 0.

All children in the subtree rooted at child 1 have key values greater than key 0 but less than key 1

All children in the subtree rooted at child 2 have key values greater than key 1 but less than key 2.

All children in the subtree rooted at child 3 have key values greater than key 2.

How do you search for a node in a 2-3-4 tree?

Similar to the search routine in the binary search tree, you start a search in a 2-3-4 tree by starting at the root and selecting sub-trees with appropriate range of values that ultimately leads to the correct node.

What are Hash Tables

Hash Tables are data structures that store data in the form of key value pairs.

Hash Tables are abstract data structures since they internally use Arrays for their implementation.

Hash Tables aim to perform the main data structure operations - insert, lookup, and delete - in constant time O(1).

Describe the structure of Hash Tables

Hash Tables are data structures that store data in the form of key value pairs.

Hash Tables internally use Arrays for their implementation.

Keys are converted into integers using a hash function, and these hashed keys are represented by the indices of the Array. Values are stored as elements of the Array at indices that equals the corresponding hashed key.

Look-ups by key on the Hash Table are performed by hashing the key and then retrieving the element of the Array at the index that equals the hashed key.

What is the role of a hash function in the implementation of Hash Tables?

Hash functions convert the key which could be a primitive data type (int, char, boolean, float, ...), Strings, or any Object type into a 32 bit int.

This converted int is used as the Array index at which the corresponding value is put.

When the value for a key has to be retrieved from the Hash Table, the key is converted into int using the same hash function, and then the value is retrieved by retrieving the element of the array at the index equal to the hashed key.

What are some common hashing techniques used the implementation of Hash Tables?

Following are some common hashing techniques used in the implementation of Hash Tables.

Division (Modulus):Hash code is generated by dividing the key by a prime number, which is also usually the size of the Array, and using the remainder as the hash code.

h(k) = k % m
Where h(k) is the hash code, k is the key, m is size of array

Multiplication: h(k)=⌊m(kAmod1)⌋

What do you understand by collision in Hash Tables?

Collisions happen in Hash Tables when two or more different keys result in the same int after going through the hash function. Hence these keys point to the same array index.

How do you resolve collisions in Hash Tables?

Collisions in Hash Tables can be resolved using following different techniques.

Open addressing

• Linear Probing
• Double Hashing
• Quadratic probing

Separate Chaining

What is load factor in Hash Tables?

Load Factor is the ratio between the number of elements present in the Hash Table to the size of Hash Table.

What is dynamic resizing in Hash Tables?

Dynamic resizing is the ability of the Hash Table to expand or contract based on the number of elements in the Hash Table.

Heaps, also referred to as Binary Heaps, are advanced data structures based on Binary Trees.

What are Heaps? Describe their structure.

Heaps are data structures that are based on binary trees. Heaps follow the following two rules.

1. The binary tree must be a complete binary tree. In a complete binary tree -

• Each node has a max of two child nodes.
• All intermediary nodes (all nodes except leaf nodes) are completely filled.
• The last level nodes (nodes containing children that are leaf nodes) must always contain a left child node.

2. The node must be ordered based on Heap property. Heap property can be one of the following.

• Min Heap.
• Max Heap.

---

What are the Heap properties used in the building of a Heap data structure?




The nodes in a Heap are build using the Heap property. Heap property can be either Min Heap or Max Heap.

Min Heap: In Min Heap the parent node keys must be less than or equal to the child node keys. Hence, in a Min Heap, the root node has the smallest key.

Max Heap: In Max Heap the parent node keys must be greater than or equal to the child node keys. Hence, in a Max Heap, the root node has the largest key.

---

What are the common application of Heap data structure?




Heap data structures are suitable for many applications and algorithms.

1. Sorting - Heapsort, one of the effieient sorting algorithm, uses Heap data structure.

2. Selection Algorithms - Selection algorithms use Heap data structures since min element or the max element can be accessed from a Heap in constant time. Others selections such as finding the median or the Kth element can be done in sub-linear time.

3. Graph Algorithms: Graph algorithms such as Prim's algorithm and Dijkstra's shortest-path algorithm uses Heaps as internal traversal data strctures.

4. Priority Queue: Priority Queue, an abstract data structure, is usually implemented with a Heap data structure.

5. K-Way merge: Heap data structures are used in K-Way merge where multiple sorted input streams are merged to a single output stream.

---

How is a Heap data structure represented in an Array?




Heap data structure is implemented using Arrays. The first element of the array contains the root node of the Heap.

The next two elements contain the two child nodes of the root. The next four elements contain the four child nodes of the two level 2 parent nodes. And so on

Building the array in above way results in the following.

• First half of the array contains the root node and intermediary nodes of the Heap
• The second half of the array contains all the leaf nodes of the Heap.

---

How do you insert a node in a Heap?




A node can be inserted into a Heap in the following way.

1. Add the new node at the end of the Heap at the first available place.

2. Check if the Heap property is violated.

3. If the Heap propert is violated then sift-up the new node until the heap property is established and the Heap is re-balanced. This is known as swim operation

---

---

How do you extract a node from a Heap?




When you extract from a Heap, the root node is removed and the Heap is reordered based on the Heap property.

A node can be extracted from a Heap in the following way.

1. Remove the root node and replace it with the last node of the Heap.

2. Check if the Heap property is violated.

3. If the Heap property is violated then sift-down the node until the heap property is established and the Heap is re-balanced. This is known as sink operation.

---

How do you replace a node from a Heap?




When you replace from a Heap, the root node is removed and replaced by the new node.

A node can be replaced from a Heap in the following way.

1. Remove the root node and replace it with the new node.

2. Check if the Heap property is violated.

3. If the Heap property is violated then sift-down the node until the heap property is established and the Heap is re-balanced (sink operation).

---

Graphs

Graphs are versatile data structures that can represent and solve for many different and unique real-world scenarios. For example - graphs can represent electronic circuit boards, roads and intersections within a city, airline routes or roadways connecting different cities, product catalogs, movies and actors etc. Due to their applicability in modeling vast number of real-world scenarios, interview questions on graphs are frequently asked in programming interviews.

---

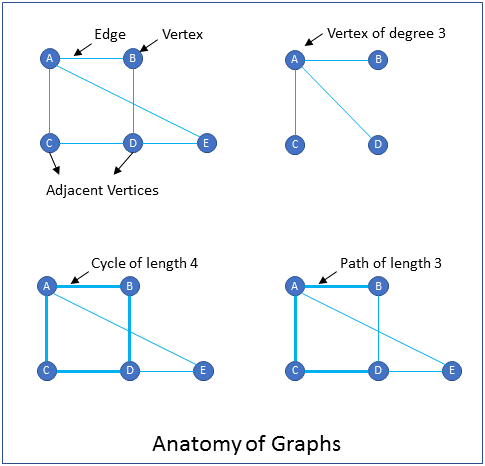
What are the components that a graph consists of?

FAQ


A graph consists of vertices and edges.

Vertices: Vertices are similar to nodes. Vertices usually have a label for identification in addition to other properties. Examples of vertices are cities in a map and pins in a circuit.

Edges: An edge connects two vertices. Examples of edges are roadways that connect cities in a map, and traces that connect pins in a circuit diagram.



---

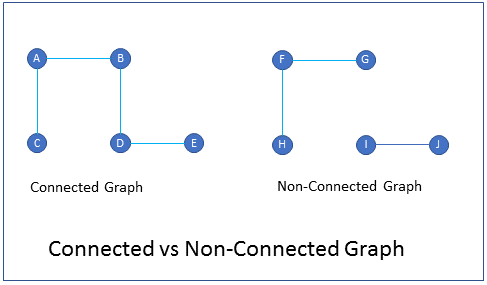
What is the difference between connected graph and non-connected graph?

FAQ


In a connected graph there is at-least one path from every vertex to every other vertex.

In a non-connected graph every vertex may not be connected to every other vertex.



---

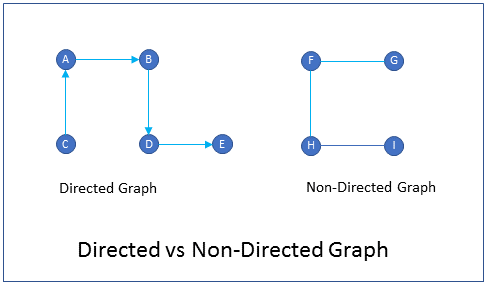
What is the difference between directed graph and non-directed graph?

FAQ


Directed graphs are graphs in which the edges have a direction. i.e. you can go from vertex A to vertex B, but you cannot go from vertex B to vertex A. An example of a directed graph is a one-way street city map. You can go only one direction on the edge (street) but not the other direction.

Non-directed graphs are graphs in which the edges do not have a direction. i.e. you can go from vertex A to vertex B and vice versa. An example of a non-directed graph is a freeway map connecting cities. You can go both directions on the edge (freeway).



---

What are weighted graphs?

FAQ


Weighted graphs are graphs in which edges are given weights to represent the value of a variable. For example in a graph of cities and freeways, the weight of an edge could represent the time it takes to drive from one city to the other. Similarly, in an airline routes graph, the weight of an edge could represent the cost of travel from one city to another.



---

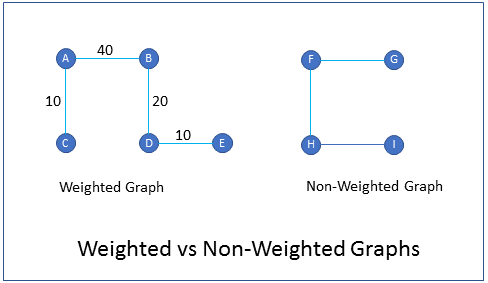
How do you represent components of a graph in a computer program?

FAQ


Components of a graph are represented as follows in a computer program.

Vertices - Vertices represent real world objects. For example, in a graph of cities and roadways the vertices represent the cities. Similarly in a graph of a circuit diagram the vertices represent the pins of the circuit board. In a computer program the vertices are modeled as classes having a variable to indicate the label of the vertex, in addition to other variables.

Edges - An edge connects two vertices. In a computer program an edge can be represented in two ways.

1. Adjacency matrix - An adjacency matrix is a NxN matrix whose elements indicate if an edge exists between two vertices. N is the number of vertices contained in the graph. Usually the value 1 is used to indicate that an edge exists between two vertices and the value 0 is used to indicate that an edge does not exist between two vertices.

2. Adjacency List - An adjacency list is an array of lists or sets that contains the adjacent vertices for each vertex of the graph. The parent list contains N elements, one element for each vertex in the graph. Each element contains a list of vertices that that are adjacent to the vertex in the element.



---

---

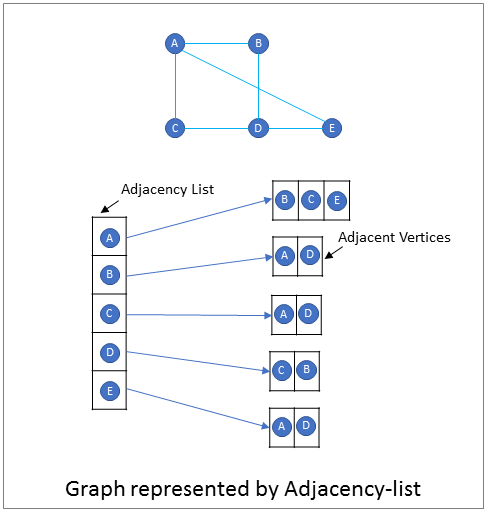
Write a program that represents a graph.

FAQ


Following is a Java program that represents a graph.

• The vertex is represented by the Vertex class and uses a char for the label.
• An array of length N maintains the list of vertices in the graph.
• An NxN adjacency matrix represents the edges, with 1 indicating that an edge exists and 0 indicating that an edge does not exist.
• The constructor takes the number of vertices as parameter and initializes the arrays.
• addVertex() and addEdge() are methods provided to add a new vertex and a new edge respectively.

//Vertex class
class Vertex{
 private char vertexLabel;
 public Vertex(char vertexLabel) {
  this.vertexLabel = vertexLabel;
 }
}

//Graph class
class Graph {
 //list of vertices
 private Vertex vertexList[];
 //adjacency matrix
 private int adjMatrix[][];
 //number of vertices
 private int nVertices;

 public Graph(int nVertices) {
  //initialize vertex list
  vertexList = new Vertex[nVertices];
  //initialize adjacency matrix
  adjMatrix = new int[nVertices][nVertices];
  for (int i=0; i<nVertices; i++) {
    for(int j=0; j<nVertices; j++) {
      adjMatrix[i][j] = 0;
    }
  }
 }

 //add a new vertex
 public void addVertex(char vertexLabel) {
  vertexList[nVertices++] = new Vertex(vertexLabel);
 }

 //add a new edge
 public void addEdge(int startVertex, int endVertex) {
  adjMartrix[startVertex][endVertex] = 1;
  adjMartrix[endVertex][startVertex] = 1;
 }

}

---

Trie

Trie, also referred to as digital tree or prefix tree, is a tree-like data structure that is used for storage and efficient retrieval of keys, usually strings.

---

1. Describe the structure, properties, and operations of a trie data structure?




Structure

Trie is similar to graph data structure. It consists of nodes, with each node containing zero or more child nodes.

Trie is similar to ordered trees where each of the children can either be null or points to another node

If words are stored in the trie data structure, then each alphabet of the word is represented by a node, with each node being a child of the previous node.

For example, the word 'the' is stored in the trie data structure as three nodes, one for each alphabet. 'h' node is a child node of 't' node, and 'e' node is a child of 'h' node.

Properties: Following are some properties of a trie data structure.

• The max number of child nodes is limited to the key type that is stored in the trie. For example, if english words are stored in the trie which is usually the case, then the max number of child nodes is 26, the number of english alphabets.
• The depth of the trie equals the max length of the key that is stored in the trie. For example if the words 'the', 'their', 'them' are stored in the trie, then the depth of the trie is 5 (number of alphabets in the longest word 'their')
• Keys with the same prefix share the same path. For example, the words 'the', 'their', 'them' have the same prefix 'the' and hence share the same path till 'e'

Operations: The key operations supported by trie data structure are:

• Insertion: Operation to insert words
• Deletion: Operation to delete words
• Seraching: Operation to retrieve words

---

2. Describe the structure of a node in a trie data structure? Write a program that represents a trie node.




Structure

A trie node represents an alphabet in a word. So if a word 'hello' is inserted into the trie then five nodes are created, each node representing an alphabet.

A trie node at a minimum contains the following data elements:

• children[]: An array of child nodes. The size of the array depends on the keys being stored in the trie. For english words the size of this array will be 26 (Number of english alphabets). By default, all elements are set to Null.
• isEndOfWord: A flag that indicates if this node represents an end of the word alphabet. For example, for the word 'hello', for the node representing the alphabet 'o' - this flag will be true.

Pseudocode

• Attributes
  • isEndOfWord
  • children[]
• Methods
  • initialization: set isEndOfWord flag to false, and initialize array to size 26.
  • markAsEnd(): This methods sets isEndOfWord flag to true
  • unmarkAsEnd(): This method sets isEndOfWord flag to false

Code

public class TrieNode {

 //indicates end of word
 public boolean isEndOfWord;
 //child nodes
 public TrieNode[] children;
 //max number of child nodes
 public static int maxChildren = 26;

//constructor
 public TrieNode() {
  this.isEndOfWord = false;
  this.children = new TrieNode[maxChildren];
 }

 public void markAsEnd() {
  this.isEndOfWord = true;
 }

 public void unmarkAsEnd() {
  this.isEndOfWord = false;
 }
}

---

3. Describe the structure of the trie class that represents the trie data structure? Write a program that represents a trie data structure.




Structure

A trie class internally uses the trie node (created in previous question) and provides functions to insert a word, delete a word, and search for a word.

A trie class contains a root note which is null, and has 26 child nodes, each of which may be null or may point to another trie node.

Pseudocode

• Attributes
  • rootNode: The starting node of the trie data structure which is always null
• Methods
  • initialization(): initialize rootNode.
  • insert(String word): Insert a word into the trie data structure.
  • delete(String word): Delete a word from the trie data structure.
  • search(String word): Search for a word in the trie data structure.

Code

public class Trie {
 //root node
 public TrieNode rootNode;

 public Trie() {
  this.rootNode = new TrieNode();
 }

 public void insert(String word) {
 }

 public void search(String word) {
 }

 public void delete(String word) {
 }
}

---

4. How do you insert a word into the trie data structure? Write a function that inserts a word into a trie data structure.




Here we will implement the logic for the insert() function that we defined in the trie class in the previous question.

Implementation logic

To insert a word into a trie data structure, we will take each character of the word, beginning from the first character, and check if it already exists in the trie path (prefix path). If it does not exist, we will add a new node to the prefix path. If it is the end of the word we will set the end of word flag to true.

Pseudocode

• Set current node to root node
• For each character of the word
• Find the index position of the character (0...25)
• Check if current node has a child node at the index position
• If not found
• Create new node at this index position
• Set current node to the child node at index position
• For the last node, set isEndOfWord flag to true.

Code

public class Trie {
 //root node
 public TrieNode rootNode;

 public Trie() {
  this.rootNode = new TrieNode();
 }

 public void insert(String word) {
  //set current node to root node
  TrieNode currentNode = rootNode;
  int position = 0;
  //for each character of the word
  for (int i = 0; i < word.length(); i++) {
   //find the index position
   position = word.charAt(i) - 'a';
   //If current node does not have a child node at the index position
   if (null == currentNode.children[position]) {
   //create new node
    currentNode.children[position] = new TrieNode();
   }
   //set current node to new child node
   currentNode = currentNode.children[position];
  }
  //mark last node as end of word
  currentNode.isEndOfWord = true;
 }

 public void search(String word) {
 }

 public void delete(String word) {
 }
}

---

5. How do you search for a word in the trie data structure? Write a function that searches for a word in a trie data structure.




Here we will implement the logic for the search() function that we defined in the trie class in the previous question.

Implementation logic

To search for a word in a trie data structure, we will take each character of the word, beginning from the first character, and check if it exists in the trie path (prefix path). If all characters exits in a prefix path, i.e. each character node is a child of the previous character node then the word exists, else the word does not exist in the trie data structure.

Pseudocode

1. Validate input word is not null
2. Set current node to root node
3. For each character of the word
  4. Find the index position of the character (0...25)
  5. Check if current node has a child node at the index position
  6. If found, set child node as the current node
  7. If not found, return false
8. Return true if endOfWord is true for the last node

Code

public boolean search(String word) {
 //1. Validate input word is not null
 if (word==null) {
  return false;
 }
 //2. Set current node to root node
 TrieNode currentNode = rootNode;
 int position = 0;
 //3. For each character of the word
 for (int i = 0; i < word.length(); i++) {
  //4. Find the index position of the character with reference to 'a' which is at index 0
  position = word.charAt(i) - 'a';
  //5. Check if current node has a child node at the index position
  if (currentNode.children[position]!=null) {
   //6. If found, set child node as the current node
   currentNode = currentNode.children[position];
  } else {
   //7. If not found, return false
   return false;
  }
 }
 //8. Return true if endOfWord is true for the last node
 return currentNode.isEndOfWord;
}

---

---

6. How do you delete a word in the trie data structure? Write a function that deletes a word in a trie data structure.




Here we will implement the logic for the delete() function that we defined in the trie class in the previous question.

Implementation logic

To delete a word in a trie data structure, we will take each character of the word, beginning from the first character, and check if it exists. If it exists and has no child nodes then we delete this node. If it exists and has child nodes, and isEndOfWord falg is true, then we set this to flag is false.

1. Validate input word is not null
2. Set current node to root node
3. For each character of the word
  4. Find the index position of the character (0...25)
  5. Check if current node has a child node at the index position
  6. If found, set child node as the current node
  7. If not found, return false
8. If current node does not have child nodes then delete node.

9. If current node has isEndOfWord flag as true, then set it to false.

Code

public boolean search(String word) {
 //1. Validate input word is not null
 if (word==null) {
  return false;
 }
 //2. Set current node to root node
 TrieNode currentNode = rootNode;
 int position = 0;
 //3. For each character of the word
 for (int i = 0; i < word.length(); i++) {
  //4. Find the index position of the character with reference to 'a' which is at index 0
  position = word.charAt(i) - 'a';
  //5. Check if current node has a child node at the index position
  if (currentNode.children[position]!=null) {
   //6. If found, set child node as the current node
   currentNode = currentNode.children[position];
  } else {
   //7. If not found, return false
   return false;
  }
 }
 //8. Return true if endOfWord is true for the last node
 return currentNode.isEndOfWord;
}

---